Mixed Numbers (or Mixed Fractions)

What are Mixed Numbers?

In a mixed number, you write the whole number first, followed by the fraction part.

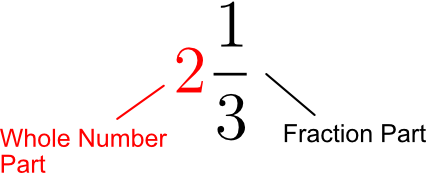
We read this as two and one-third, or two, one over three [insert a slight pause between the whole number and fractional parts].

As you may have realized, mixed fractions are used to denote quantities that contain both whole things and parts of a whole.

Mixed Numbers and Improper Fractions

In the picture below, we have one and a half pizzas on both sides. Now, when we say one and a half, we are talking about the whole (one) and the remaining part (a half) separately. That’s how mixed numbers work.

But there’s also another way of expressing the same quantity.

We could have said three halves of pizzas and that would mean the same thing. Here we are talking about the entire quantity in terms of parts (halves). One whole is made up of two halves, isn’t it?

So mixed numbers can also be expressed as (pure) fractions. And those fractions will always be improper or top-heavy fractions.

Now let’s see how we can convert mixed numbers into improper fractions and vice-versa. It will also help you better understand the relationship between them.

How to Convert Mixed Numbers into Improper Fractions

Let me explain using the following example.

Solution

Here’s an illustration showing how we use the rules mentioned above to convert a mixed number into an improper fraction.

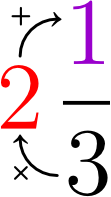
So,

Done.

How This Works

Say there are $\hspace{0.2em} 2 \frac{1}{3} \hspace{0.2em}$ pizzas. So, $\hspace{0.2em} 2 \hspace{0.2em}$ full pizzas and another one-third.

To convert this into a mixed number, we need to talk only in terms of the fractional part — the thirds. So how many thirds of a pizza are there?

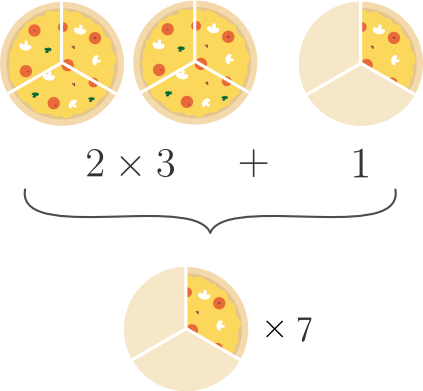
Well, each whole pizza has $\hspace{0.2em} 3 \hspace{0.2em}$ thirds. So there would be $\hspace{0.2em} 2 \hspace{0.2em}$ times $\hspace{0.2em} 3 \hspace{0.2em}$, $\hspace{0.2em} 6 \hspace{0.2em}$ thirds, in two pizzas. But there’s also the extra one-third. So altogether, $\hspace{0.2em} 7 \hspace{0.2em}$ thirds. Or $\hspace{0.2em} \frac{7}{3} \hspace{0.2em}$ pizzas.

Well, that’s exactly what we did in the example above. Didn’t we?

Solution

Like we did in the last example,

Converting Improper Fractions into Mixed Numbers

Solution

Step 1. Divide the numerator by the denominator.

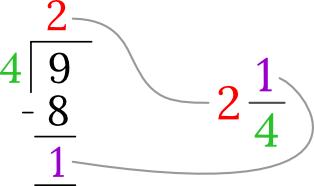
Step 2. Write the mixed fraction. The quotient becomes the whole number part and the remainder becomes the numerator. The denominator remains the same as that in the improper fraction.

So,

And thus we have converted the improper fraction into a mixed fraction.

How This Works

Say you have nine-quarters of a pizza.

So how many whole pizzas can you make out of them? And how many quarters will remain unused?

Well, to make $\hspace{0.2em} 1 \hspace{0.2em}$ whole pizza, you need $\hspace{0.2em} 4 \hspace{0.2em}$ quarters. So the real question is — how many times can you take $\hspace{0.2em} 4 \hspace{0.2em}$ out of $\hspace{0.2em} 9 \hspace{0.2em}$ (we have $\hspace{0.2em} 9 \hspace{0.2em}$ quarters), and what will be the remainder?

To find the answer, we divide $\hspace{0.2em} 9 \hspace{0.2em}$ by $\hspace{0.2em} 4 \hspace{0.2em}$.

Now, $\hspace{0.2em} 4 \hspace{0.2em}$ goes into $\hspace{0.2em} 9 \hspace{0.2em}$ twice (so $\hspace{0.2em} 2 \hspace{0.2em}$ whole pizzas) and leaves $\hspace{0.2em} 1 \hspace{0.2em}$ as the remainder (so $\hspace{0.2em} 1 \hspace{0.2em}$ extra quarter).

In other words, you have $\hspace{0.2em} 2 \frac{1}{4} \hspace{0.2em}$ pizzas.

Solution

Like we did in the previous example, we start by dividing the numerator by the denominator.

So,

Negative Mixed Numbers

Negative mixed numbers sometimes cause confusion among students. They have questions like – is the negative sign only for the whole number part only or the entire mixed number? Or how to convert them into improper fractions?

Negative sign before a mixed number

• The negative sign is for the mixed fraction in totality, meaning –

$$-1 \frac{2}{3} = - \left ( 1 \frac{2}{3} \right )$$

• So, here’s how you convert a negative mixed number into an improper fraction.

Operations on Mixed Numbers

Generally, to perform any operations on mixed numbers, you need to convert them into improper fractions.

Let’s look at a couple of examples.

Solution (a)

Here, we have a subtraction involving a mixed fraction. So we start by converting it into an improper fraction.

And now, it’s the usual case of subtracting fractions.

Note how I converted the answer back into a mixed number. If the question uses mixed numbers and not improper fractions, you must not leave an improper fraction in your answer either. Convert it into a mixed number.

Solution (b)

Again, in the first step, we convert the mixed fraction into an improper fraction. And then proceed to multiply the two pure fractions.

And with that, we come to the end of this tutorial. Until next time.