Improper Fractions - A Complete Tutorial

A fraction has two essential components – the numerator (top number) and the denominator (bottom number). Depending on whether the numerator is less than, equal to, or greater than the denominator, fractions are classified as “proper” or “improper”.

In this tutorial, we will focus on improper fractions.

What are Improper Fractions?

An improper fraction is a fraction in which the numerator (top number) is equal to or greater than the denominator (bottom number). For example - $\hspace{0.2em} \frac{3}{2} \hspace{0.2em}$ , $\hspace{0.2em} \frac{4}{4} \hspace{0.2em}$ , and $\hspace{0.2em} \frac{15}{7} \hspace{0.2em}$ .

Improper fractions are also called top-heavy fractions.

On the other hand, fractions with numerators less than their denominators are known as proper fractions. For example - $\hspace{0.2em} \frac{1}{2} \hspace{0.2em}$ , $\hspace{0.2em} \frac{5}{8} \hspace{0.2em}$ , and $\hspace{0.2em} \frac{7}{12} \hspace{0.2em}$

Now you might ask, why do we care whether the top number is less than, equal to, or greater than the bottom number? Good question.

Let me explain.

Why It Matters

The denominator in a fraction indicates the total number of equal parts that make a whole. So, if we take the example of a pizza, a denominator of $\hspace{0.2em} 6 \hspace{0.2em}$ would indicate the pizza is divided into $\hspace{0.2em} 6 \hspace{0.2em}$ equal slices.

Now, as long as a fraction represents less than $\hspace{0.2em} 6 \hspace{0.2em}$ such slices (the top number is smaller than $\hspace{0.2em} 6 \hspace{0.2em}$ ), those slices won’t add up to give a whole pizza.

That’s why proper fractions always represent values less than $\hspace{0.2em} 1 \hspace{0.2em}$ . Their numerators are always smaller than their denominators.

With improper fractions, it’s the opposite. The numerator is either equal to or greater than the denominator.

When the top and bottom numbers are equal, the value is exactly $\hspace{0.2em} 1 \hspace{0.2em}$ .

When the top number is greater, the value is greater than $\hspace{0.2em} 1 \hspace{0.2em}$ .

So, improper fractions always represent values greater than $\hspace{0.2em} 1 \hspace{0.2em}$ (unless they are negative).

And that’s what connects improper fractions to mixed numbers. More on that below.

Improper Fractions and Mixed Numbers

In the picture below, we have the same quantity of pizza on both sides. But we can talk about it in different ways. We can say we have $\hspace{0.2em} 3 \hspace{0.2em}$ halves of a pizza or simply one and a half pizzas.

Three-halves or one and a half - different ways to express the same quantity

It depends on how we look at “whole” things. If we consider them a group of smaller parts (halves, thirds etc.) and count those parts, we end up with improper fractions.

But if we consider each whole as a single unit and count them separately from the extra parts, we get mixed numbers.

In short, improper fractions and mixed numbers are just two different ways of expressing the same quantity. And both are correct.

In the next sections, you’ll learn how to convert improper fractions into mixed numbers and vice-versa. It will also help you better understand the relationship between them.

Converting Improper Fractions into Mixed Numbers

To convert an improper fraction into a mixed number –

Divide the numerator by the denominator.

The quotient becomes the whole number part of the mixed number.
The remainder becomes the numerator.

Copy the denominator from the improper fraction.

Example

Convert the improper fraction, $\hspace{0.2em} \frac{7}{3} \hspace{0.2em}$ , into a mixed number.

Solution

Step 1. Divide the numerator by the denominator.

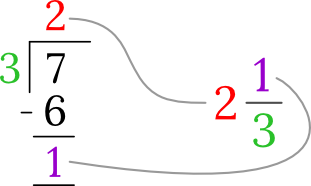
How to convert improper fractions into mixed numbers — Steps 1 (Left) and 2 (Right)

Step 2. Write the mixed number using the quotient as the whole number part and the remainder as the numerator. Copy the denominator from the improper fraction.

So,

\frac{7}{3} = 2 \frac{1}{3}

That’s it. You have converted the improper fraction into a mixed number.

How This Works

Say you have seven-thirds of a pizza.

So how many whole pizzas can you make out of them and how many thirds will remain unused?

Well, to make $\hspace{0.2em} 1 \hspace{0.2em}$ whole pizza, you need $\hspace{0.2em} 3 \hspace{0.2em}$ thirds. So the real question is — how many times can you take $\hspace{0.2em} 3 \hspace{0.2em}$ out of $\hspace{0.2em} 7 \hspace{0.2em}$ (we have $\hspace{0.2em} 7 \hspace{0.2em}$ thirds, remember?), and what will be the remainder?

To find the answer, we divide $\hspace{0.2em} 7 \hspace{0.2em}$ by $\hspace{0.2em} 3 \hspace{0.2em}$ .

So, $\hspace{0.2em} 3 \hspace{0.2em}$ goes into $\hspace{0.2em} 7 \hspace{0.2em}$ two times (so $\hspace{0.2em} 2 \hspace{0.2em}$ full pizzas) and leaves $\hspace{0.2em} 1 \hspace{0.2em}$ as the remainder (so $\hspace{0.2em} 1 \hspace{0.2em}$ extra quarter). So, $\hspace{0.2em} 2 \frac{1}{3} \hspace{0.2em}$ pizzas.

Example

Convert the mixed number, $\hspace{0.2em} \frac{23}{7} \hspace{0.2em}$ , into a mixed number.

Solution

Just as we did in the previous example, we divide the numerator by the denominator.

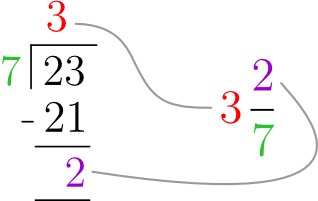
And that gives us our mixed number.

\frac{22}{5}=4 \frac{2}{5}

Converting Mixed Fractions to Improper Fractions

To convert a mixed number into an improper fraction –

Multiply the denominator with the whole number part and add the numerator to the product.
The result from above is your numerator.
The denominator remains the same.

Let me explain using the following example.

Example

Convert the mixed number, $\hspace{0.2em} 2 \frac{1}{4} \hspace{0.2em}$ , into an improper fraction.

Solution

To get the numerator of the improper fraction, we multiply the denominator with the whole number part and add the numerator.

The denominator remains the same. So,

\begin{align*}2 \frac{1}{3} &= \frac{3 \times 2 + 1}{3} \\[0.5cm] &= \frac{7}{3} \end {align*}

How This Works

Say you have $\hspace{0.2em} 2 \frac{1}{4} \hspace{0.2em}$ pizzas. So, $\hspace{0.2em} 2 \hspace{0.2em}$ full pizzas and an extra quarter.

To get the improper fraction representing the same quantity of pizza, we need to be talking only in terms of the fractional part — the quarters. So how many quarters of a pizza do you have?

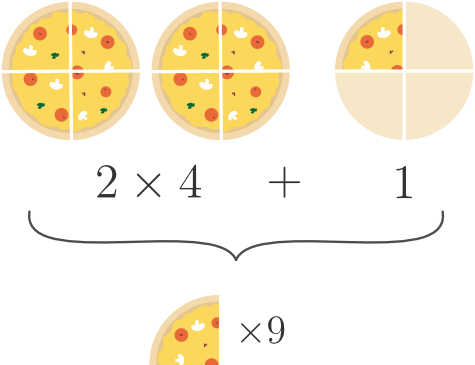
Well, each whole pizza has $\hspace{0.2em} 4 \hspace{0.2em}$ quarters. So $\hspace{0.2em} 2 \hspace{0.2em}$ pizzas will have $\hspace{0.2em} 2 \hspace{0.2em}$ times $\hspace{0.2em} 4 \hspace{0.2em}$ , $\hspace{0.2em} 8 \hspace{0.2em}$ quarters. But you also have one extra. So altogether, $\hspace{0.2em} 9 \hspace{0.2em}$ quarters. Or $\hspace{0.2em} \frac{9}{4} \hspace{0.2em}$ pizzas.

Isn’t this the same as what we did in the example earlier?

Example

Convert the mixed number, $\hspace{0.2em} 4 \frac{3}{7} \hspace{0.2em}$ , into an improper fraction.

Solution

Just as we did in the last example –

\begin{align*} {\color{Red} 5} \frac{ {\color{Teal} 2} }{7} &= \frac{ {\color{Red} 5} \times 7 + {\color{Teal} 2} }{3} \\[0.5cm] &= \frac{37}{7} \end {align*}

Are Improper Fractions Bad?

We are generally expected to convert any improper fractions in our answers into mixed numbers – unless the question itself uses improper fractions. This makes some students believe that there is something wrong with improper fractions.

That's not true.

There is nothing wrong, incorrect, or bad about improper fractions. You are encouraged to express improper fractions as mixed numbers only because mixed numbers are easier to visualize and hence easier to understand.

For example, $\hspace{0.2em} 5 \frac{1}{3} \hspace{0.2em}$ is the same as $\hspace{0.2em} \frac{16}{3} \hspace{0.2em}$ . Yet, looking at the mixed number, you can quickly see we are talking about $\hspace{0.2em} 5 \hspace{0.2em}$ and a little more. With the improper fraction, it’s not so obvious.

At the same time, it is generally easier to perform operations on improper fractions. So we convert mixed numbers into improper fractions if we need to add, subtract, or do any other operations on them.

And with that, we come to the end of this tutorial on improper fractions. Until next time.