How to Simplify Fractions

What Does It Mean to Simplify Fractions?

To simplify a fraction (or reduce it to its lowest terms) means to rewrite it such that its top and bottom numbers have no common factors (other than 1, of course).

To simplify a fraction, you must cancel out all the common factors between the numerator and the denominator. You can do that by dividing them both by their GCF.

Simplifying a fraction is also referred to as reducing the fraction to its simplest form.

Now let’s look at the different ways to simplify fractions in greater detail.

How to Simplify Fractions?

As mentioned earlier, to simplify a fraction, we must get rid of all the common factors between the numerator and the denominator. There are 3 methods to do this. We’ll look at each of them, one by one.

Prime Factorization

In this method, you factorize the numerator and the denominator into prime factors (hence splitting them into smaller factors) and then cancel out the common factors.

Example

Simplify the fractions.

(a) \hspace{0.3cm} \frac{72}{90}

(b) \hspace{0.3cm} \frac{25}{125}

Solution (a)

Step 1. We start with the prime factorization of the top and bottom numbers.

\frac{72}{90} = \frac{2 \times 2 \times 2 \times 3 \times 3}{2 \times 3 \times 3 \times 5}

Step 2. Cancel out the factors that are common to the top and bottom groups (one $\hspace{0.2em} 2 \hspace{0.2em}$ and two $\hspace{0.2em} 2 \hspace{0.2em}$ s).

\begin{align*} \frac{72}{90} &= \frac{\cancel{2} \times 2 \times 2 \times \cancel{3} \times \cancel{3}}{\cancel{2} \times \cancel{3} \times \cancel{3} \times 5} \\[1.3em] &=\frac{2 \times 2}{5} \hspace{0.25em} = \hspace{0.25em} \frac{4}{5} \end{align*}

Step 3. As shown above, multiply the factors remaining after cancelation, to get the fraction in its simplest form.

Solution (b)

Again, we follow the same steps – prime factorization followed by the cancelation.

\begin{align*} \frac{25}{125} &= \frac{\cancel{5} \times \cancel{5}}{\cancel{5} \times \cancel{5} \times 5} \\[1.3em] &=\frac{1}{5} \end{align*}

But there’s also something interesting here. After we canceled the common factors, it looked like we didn’t have anything left at the top.

But remember, when all factors get canceled, there’s always a “ $\hspace{0.2em} 1 \hspace{0.2em}$ ” hidden there ( $\hspace{0.2em} 5 \hspace{0.2em}$ divided or canceled by $\hspace{0.2em} 5 \hspace{0.2em}$ gives $\hspace{0.2em} 1 \hspace{0.2em}$ , right?) and that $\hspace{0.2em} 1 \hspace{0.2em}$ became the numerator in our final fraction.

Why prime factorization?

When you factorize a number into its prime factors, you reduce it to the lowest level, into the smallest factors. You can’t go any further. So, in one step, you can see all the factors that are common to the numerator and the denominator and cancel them out.

Prime factorization makes things easier and reduces the chances of making errors. At least, when you have just learned how to simplify fractions.

Dividing by the GCF

This is the most straightforward of the three methods we discuss in this article.

In this method, we divide the top and bottom numbers by their GCF (Greatest Common Factor). The result is our fraction in its lowest terms.

Example

Reduce the fractions to their lowest terms.

(a) \hspace{0.3cm} \frac{72}{90}

(b) \hspace{0.3cm} \frac{25}{125}

Solution (a)

The first step would be to find the GCF of $\hspace{0.2em} 24 \hspace{0.2em}$ and $\hspace{0.2em} 42 \hspace{0.2em}$ , which comes out to be $\hspace{0.2em} 6 \hspace{0.2em}$ .

In the next step, we divide the top and bottom numbers by their GCF.

\begin{align*} \frac{24}{42} &= \frac{24 \div 6}{42 \div 6} \\[1.3em] &= \frac{4}{7} \end{align*}

And we have reduced the fraction to its lowest terms.

Solution (b)

The GCF of $\hspace{0.2em} 45 \hspace{0.2em}$ and $\hspace{0.2em} 72 \hspace{0.2em}$ is $\hspace{0.2em} 9 \hspace{0.2em}$ . So,

\begin{align*} \frac{45}{42} &= \frac{45 \div 9}{72 \div 9} \\[1.3em] &= \frac{5}{8} \end{align*}

Repeated Division

In this method, we divide the numerator and denominator by any common factor we can find. And we repeat this until we run out of common factors.

Example

Reduce the fractions to their simplest forms.

(a) \hspace{0.3cm} \frac{60}{120}

(b) \hspace{0.3cm} \frac{24}{36}

Solution (a)

Alright, one factor is obviously common between $\hspace{0.2em} 60 \hspace{0.2em}$ and $\hspace{0.2em} 120 \hspace{0.2em}$ . That’s $\hspace{0.2em} 10 \hspace{0.2em}$ .

So let’s divide both the numbers by 10.

\frac{60}{120} = \frac{60 \div 10}{120 \div 10} = \frac{6}{12}

Now our fraction is simpler than what we started but we can simplify further. $\hspace{0.2em} 6 \hspace{0.2em}$ is a common factor of $\hspace{0.2em} 6 \hspace{0.2em}$ and $\hspace{0.2em} 12 \hspace{0.2em}$ , so we divide them both by $\hspace{0.2em} 6 \hspace{0.2em}$ .

\frac{6}{12} = \frac{6 \div 6}{12 \div 6} = \frac{1}{2}

And there are no more common factors left. So the fraction is now in its simplest form.

Now unless it is a test, where you need to show every step, you don’t have to do all the writing you see above. And that’s what makes this method so amazing.

Here’s how you do it. You do the divisions in your head and write only the results.

Short, simple, and quick. The only thing is you may need to brush up on your numbers skills. Most importantly, multiplication tables and divisibility rules.

Also, there’s no rule as to which factors you must use or the number of steps involved. So, for example, we could have done the above simplification in three steps – canceling $\hspace{0.2em} 10 \hspace{0.2em}$ , $\hspace{0.2em} 2 \hspace{0.2em}$ , and finally $\hspace{0.2em} 3 \hspace{0.2em}$ .

Here’s how that would look.

Solution (b)

Alright, let’s do this one using our condensed format. We will do the simplification in two steps – first, we cancel $\hspace{0.2em} 4 \hspace{0.2em}$ , and then $\hspace{0.2em} 3 \hspace{0.2em}$ .

Done.

Now, of course, we could have done it in one step too, canceling $\hspace{0.2em} 12 \hspace{0.2em}$ in the first step itself.

Anyway, I guess you can already see why I love this method, as do most people comfortable with numbers.

So, we have covered three different methods you can use to simplify fractions. Practice each method and then decide which one you like most.

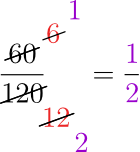
$How to simplify fractions by successive division$

And with that, we come to the end of this tutorial. Until next time.

Frequently Asked Questions

Why do we simplify fractions at all?

By simplifying fractions, we make the its top and bottom numbers smaller without changing the value of the fraction. That makes adding, subtracting or just working with fractions in general, much easier.

As an example, consider the fraction, $52/78$ . If you reduce it to its lowest terms, it becomes $2/3$ . The two fractions are the same in value. But which one is easier to make sense of? Or to work with?

How does the simplified fraction have the same value?

Here's the thing. Dividing (or multiplying) the numerator and denominator of a fraction by the same number doesn't change the value of the fraction. It just gives a fraction equivalent to the original.