Equivalent Fractions — How to Find/Check Equivalent Fractions

What are Equivalent Fractions?

Equivalent fractions are fractions with the same value even though they have different top and bottom numbers.

For example – $\hspace{0.2em} \frac{1}{3} \hspace{0.2em}$ , $\hspace{0.2em} \frac{2}{6} \hspace{0.2em}$ , and $\hspace{0.2em} \frac{3}{9} \hspace{0.2em}$ . They are all equivalent to one another.

If you multiply or divide the numerator (top) and denominator (bottom) of a fraction by the same number, you get a fraction equivalent to the original one.

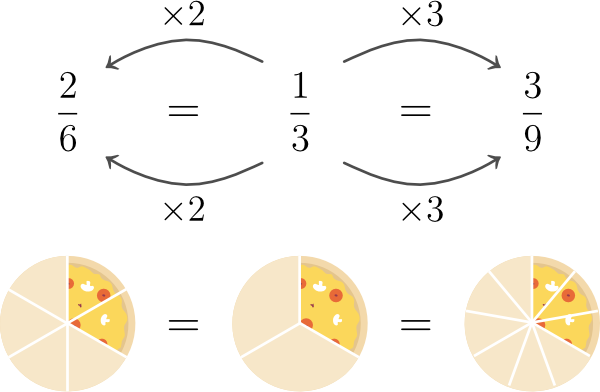
Three equivalent fractions - 1/3, 2,6, and 3/9. And their pizza diagrams. — Three equivalent fractions – One value

How to Find Equivalent Fractions?

As mentioned above, you can produce equivalent fractions from a given fraction by multiplying (or dividing) its numerator and denominator by the same number.

Example

Find fractions equivalent to —

(a) \hspace{0.3cm} \frac{2}{5}

(b) \hspace{0.3cm} \frac{1}{4}

Solution (a)

Let’s multiply the top and bottom numbers by $\hspace{0.2em} 2 \hspace{0.2em}$ to get one equivalent fraction and then by $\hspace{0.2em} 3 \hspace{0.2em}$ to get another.

\begin{align*} \frac{2}{5} = \frac{2 \times 2}{5 \times 2} = \frac{4}{10} \\[1.75em] \frac{2}{5} = \frac{2 \times 3}{5 \times 3} = \frac{6}{15} \end{align*}

That’s it. We have found two equivalent fractions for $\hspace{0.2em} \frac{2}{5} \hspace{0.2em}$ .

Note — We could have chosen any two numbers, we went with $\hspace{0.2em} 2 \hspace{0.2em}$ and $\hspace{0.2em} 3 \hspace{0.2em}$ because they are small and so, multiplication is easier. One could also divide instead of multiplying, but in most cases, multiplication offers the easier route.

Solution (b)

This time let’s multiply by $\hspace{0.2em} 3 \hspace{0.2em}$ and $\hspace{0.2em} 6 \hspace{0.2em}$ to get the required equivalent fractions.

\begin{align*} \frac{1}{4} = \frac{1 \times 3}{4 \times 3} = \frac{3}{12} \\[1.75em] \frac{1}{4} = \frac{1 \times 6}{4 \times 6} = \frac{6}{24} \end{align*}

How This Works

In the picture above the circle is divided into three equal parts and one of those parts is shaded (dark blue). So we can represent the shaded region by the fraction, $\hspace{0.2em} \frac{1}{3} \hspace{0.2em}$ .

Let’s see what happens if we split each part (the “thirds”) into 2 equal parts.

Now the total number of equal parts making the circle becomes 6 – 2 times what it was. At the same time, the number of shaded parts also undergoes the same change – it becomes 2 (2 times 1).

So, we have a new fraction for the same shaded region.

The key takeaway is – as long as the total number of parts that make up a whole (the denominator) and the number of parts shaded (numerator) increase or decrease by the same factor, the fraction’s value remains the same.

How to Check Whether Two Fractions Are Equivalent or Not?

To check whether two fractions are equivalent, cross multiply – taking the numerator of one fraction and the denominator of the other. If you get the same answer (product) for both pairs, the two fractions are equivalent.

Example

Check if the following pairs of fractions are equivalent.

(a) \hspace{0.3cm} \frac{1}{2} \hspace{0.1cm},\hspace{0.1cm} \frac{4}{8}

(b) \hspace{0.3cm} \frac{2}{3} \hspace{0.1cm},\hspace{0.1cm} \frac{3}{4}

Solution (a)

Let’s cross-multiply and check.

\begin{align*} \frac{ {\color{Red} 1} }{2} &\stackrel{?}{=} \frac{4}{ {\color{Red} 8} } \\[1.3em] \Rightarrow {\color{Red} 1} \times {\color{Red} 8} &\stackrel{?}{=} 2 \times 4 \\[1.3em] \Rightarrow \hspace{1.8em} 8 &= 8 \end{align*}

In the end, the two sides prove to be equal. Hence, the two fractions are equivalent.

Solution (b)

\begin{align*} \frac{ {\color{Red} 2} }{3} &\stackrel{?}{=} \frac{3}{ {\color{Red} 4} } \\[1.3em] \Rightarrow {\color{Red} 2} \times {\color{Red} 4} &\stackrel{?}{=} 3 \times 3 \\[1.3em] \Rightarrow \hspace{1.7em} 8 &\neq 9 \end{align*}

In the end, the two sides prove not to be equal. Hence, the two fractions are not equivalent.

Alternate Method

Find the number by which you must multiply (or divide) one numerator to change it into the other.
Does the same transformation work for the denominators too? If yes, the fractions are equivalent. Otherwise, not.

Example

Check if the following pairs of fractions are equivalent.

(a) \hspace{0.3cm} \frac{2}{3} \hspace{0.1cm},\hspace{0.1cm} \frac{4}{6}

(b) \hspace{0.3cm} \frac{3}{5} \hspace{0.1cm},\hspace{0.1cm} \frac{9}{10}

Solution (a)

As you can see below, if we multiply the first numerator by 2, we get the second numerator. And this same operation works for the denominators too. If we multiply the first denominator by 2, we get the second denominator.

So, in this case, it is indeed a pair of equivalent fractions.

Solution (b)

In this example, to change the first numerator into the second, we must multiply it by 3. But this doesn’t work for the denominators. There, we need to multiply the first by 2 to get the second (multiplying by 3 will give us 15 instead of 10).

So, these are not equivalent fractions.

Example

Are $\hspace{0.2em} \frac{4}{5} \hspace{0.2em}$ and $\hspace{0.2em} \frac{11}{15} \hspace{0.2em}$ equivalent fractions?

Solution

It’s not always necessary to know the exact transformations that connect the top or bottom numbers. Often, you can tell the two transformations would be different even if you don’t know what exactly they are.

For example, in our case here, the second denominator is 3 times the first. But when you look at the numerators, it’s clear that the second is certainly not 3 times the first (4 times 3 would be 12 and not 11).

So the fractions are not equivalent.

How Are Equivalent Fractions Useful?

Great question. Let me give you two simple reasons.

When working with two or more fractions (like adding, subtracting, or comparing), things are much easier if each fraction has the same denominator. So we often make the denominators equal by finding a suitable equivalent fraction for each fraction in the group.

We simplify fractions (reduce them to their lowest terms) all the time. Why is it that simplified fractions have the same value as the original one? Now you know the answer. The two fractions are equivalent.
In fact, if you take a group of equivalent fractions and simplify them, they will each reduce to the same fraction.

And with that, we come to the end of this tutorial. Until next time.