Equivalent Fractions Calculator

Choose your calculator☝️

Find fractions equivalent to

Please provide your input and click the calculate button

About the Equivalent Fractions Calculator

The equivalent fractions calculator can find fractions equivalent to a given fraction. It can also check which fractions from a group are equivalent.

Usage Guide

Hide

i. Valid Inputs

Find — To find equivalent fractions, enter a single fraction (or integer or mixed number). Here are examples of fractions and mixed numbers.

Fractions → $\hspace{0.2em} 2/3 \hspace{0.2em}$ , $\hspace{0.2em} -1/5 \hspace{0.2em}$
Mixed numbers → $\hspace{0.2em} 5 \hspace{0.5em} 1/4 \hspace{0.2em}$ , $\hspace{0.2em} -2 \hspace{0.5em} 3/7 \hspace{0.2em}$

Check — When the "Check" tab is selected, you can enter a list of upto 10 fractions (or integers or mixed numbers). The calculator will find which of the fractions in the list are equivalent.

ii. Example

If you would like to see an example of the calculator's working, just click the "example" button.

iii. Share

We would love to see you share our calculators with your family, friends, or anyone else who might find it useful.

By checking the "include calculation" checkbox, you can share your calculation as well.

Here's a quick overview of what equivalent fractions are, how to find them for a given fraction, and how to check if two fractions are equivalent.

For those interested, we have a more comprehensive tutorial on equivalent fractions.

Equivalent Fractions

Equivalent fractions are fractions with the same value even though they have different top and bottom numbers.

For example — $1/3, 2/6, 3/9$ . They are all equivalent to one another.

Here's an illustration that should help make concept clearer. Also, it'll make more sense once we get to the next section.

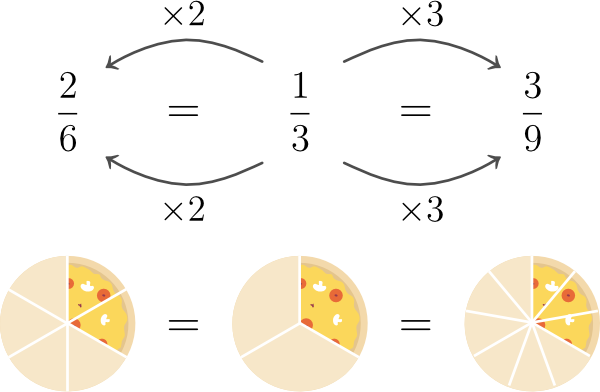
Three equivalent fractions - 1/3, 2,6, and 3/9. And their pizza diagrams. — Three equivalent fractions – One value

Finding Equivalent Fractions

You can generate equivalent fractions from a given fraction by multiplying (or dividing) its numerator and denominator by the same number.

Example

Find two fractions equivalent to $5/9$ .

Solution

Let’s multiply the top and bottom numbers by $\hspace{0.2em} 2 \hspace{0.2em}$ to get one equivalent fraction and then by $\hspace{0.2em} 3 \hspace{0.2em}$ to get another.

\begin{align*} \frac{5}{9} = \frac{5 \times {\color{Red} 2} }{9 \times {\color{Red} 2} } = \frac{10}{18} \\[1.75em] \frac{5}{9} = \frac{5 \times {\color{Teal} 3} }{9 \times {\color{Teal} 3} } = \frac{15}{27} \end{align*}

That’s it. We have found two equivalent fractions for $\hspace{0.2em} 5/9 \hspace{0.2em}$ .

Are the Two Fractions Equivalent?

The most common way to check if two fractions are equivalent is to cross multiply — taking the numerator of one fraction and the denominator of the other. If you get the same answer (product) for both pairs, the two fractions are equivalent.

Example

Are $2/3$ and $4/5$ equivalent fractions?

Solution

Let’s cross-multiply and check.

\begin{align*} \frac{ {\color{Red} 2} }{3} &\stackrel{?}{=} \frac{4}{ {\color{Red} 5} } \\[1.3em] \Rightarrow \hspace{0.25em} {\color{Red} 2} \times {\color{Red} 5} &\stackrel{?}{=} 3 \times 4 \\[1.3em] \Rightarrow \hspace{1.55em} 10 &\neq 12 \end{align*}

In the end, the two sides prove not to be equal. Hence, the two fractions are not equivalent.